А я, видимо, накосячил. Или большие погрешности в привидении типов. ))
Только сейчас обратил внимание, что при разных значениях kof выходные значения не меняются )))
позволю полюбопытствовать чем 0,3 отличается от 0.7 а то я не увидел
Читай выше!!!
так попроще наверное
2 лайка
Проще то это да. Я не понимаю почему при разных kof одни и теже значения.
Грешу на погрешность вычисления и привидения типов… (
ЗЫ: У тебя же получается просто парабола, а я хотел её пологость менять…
ЗЫ2: Видимо на таких значениях иначе и не получится. Предлагаю за решение отметить #44. Он проще. А моё решение всё равно никаких “плюшек” не имеет.
Потому что ты их нормируешь на один и тот же диапазон
И есть решение какое? Или это «тупик»?
Коэффициент надо применять только к значению, а к максимуму не надо.
Так что в строке 34 kof оставь, а в 35 убери.
так мы ТС убьём на его лисапеде
1 лайк
Убивать никого не надо!!!
Лучше мирить все мои платы!
Уж очень на рынке всё дорого!
Я ведь так тоже думал и пробовал. Тогда максимальное значение сильно меньше получается от 180 (у меня получалось 18).
Максимум конечно будет меньше, он должен быть kof*180.
Это нормально.
Иначе никак.
Я завтра перегружу и проверю на стенде (без веса своего тела (64кг))!!!
А как же тогда добиться пологой параболы, но с максимальным значением?
ты хочешь сказать эллиптической кривой?
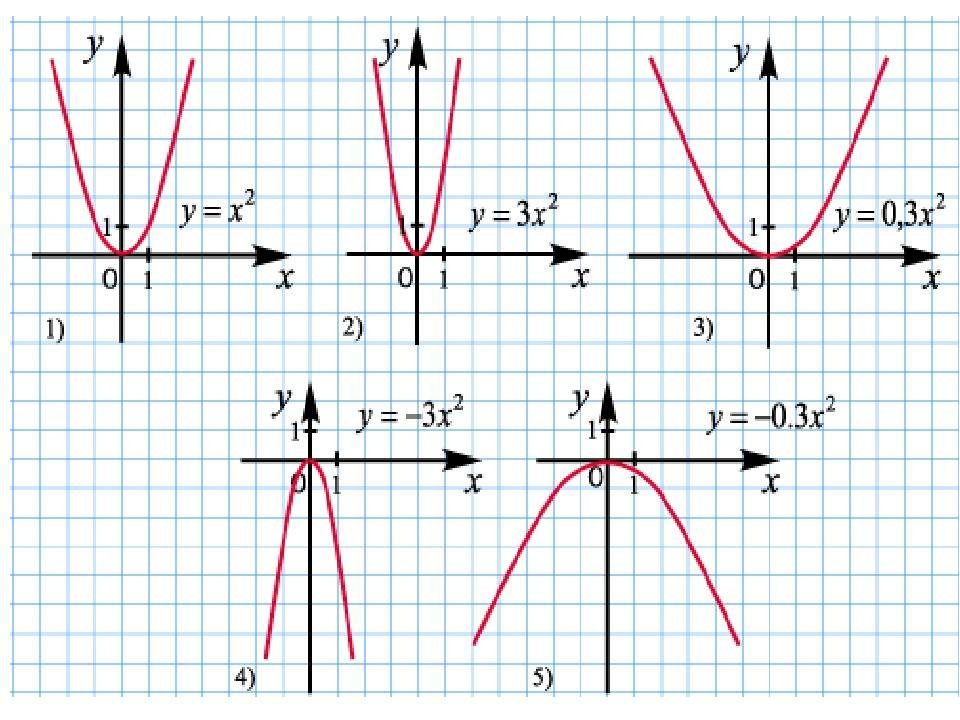
Нет никакой “пологой” параболы.
Парабола, y =ax2 проходящая через точки 0,0 и 1023,180 - одна единственная.
Чтобы получить другие, надо переходить на уравнение y =ax**2 +bx+c и подбирать коэффициенты
А как это правильно называется (верхний ряд)?
Это все параболы. Но через заданную точку 1023,180 пройдет только одна из них.
Когда меняешь свой коэф, ты уходишь с этой точки. А потом используешь функцию map() для подгонки результата и фактически получаешь ту же самую единственную кривую. Поэтому у тебя значения от коэф и не зависели.
1 лайк
Чтобы получить более пологую кривую, можно взять степень меньше, например вместо квадрата 1,5 или 1,3. Но для АВР это тяжёлая математика.
Поправка. Выше неправильно.