Приветствую!
Суть задачи: Нужно как-то организовать хранение GPS-координат для автопилота.
Есть река. Она может разветвляться на несколько русел и снова сходится.
Я посидел вечерок-другой и набросал маршрут на реке = последовательность точек. Точка = широта и долгота. Получилось 18 файлов по 10-50 точек в каждом файле. Каждый файл имеет свое имя(номер).
Там где одно русло - файлы идут друг за другом по нумерации. Там где разветвление, сначала идет файл с основным руслом, потом несколько фалов по ответвлению, потом опять файлы основного русла.
При включении автопилота нужно определить файл где мы находимся - т.е. к какой точке ближе всего. Далее идем от точки к точке по этому файлу. Как файл закончился, берем следующий по номеру и смотрим рядом ли мы с первой координатой из этого файла. Если да - идем по этому файлу, если нет - берем следующий.
Вопрос вот в чем: как грамотно организовать хранение данных так чтобы поиск ближайшей точки из файла занимал минимум времени?
0 секунд?
При правильной организации размер файла не должен превышать 512 байт. Это - размер сектора. Файл хранится на накопителе и читается посекторно.
Основное время при доступе будет занимать именно процедура чтения (если речь идет о файловом доступе, вероятно, возникнет необходимость читать несколько секторов).
То есть самое первое, что нужно сделать - оптимизировать алгоритм с точки зрения открытия/закрытия файлов.
Вывод: данные организованы неоптимально уже на этапе проектирования (18 файлов).
1 координата занимает 40 байт 40 × 50 × 18=36 000 мегабайт))) и следовательно точно sd карта как я понял будет…
и вот для этого дела выложите ка пж код))) а там может и подскажут, он ведь есть ? или это из разряда сделайте за меня ?
а так если с sd карты, то напишите алгоритм сравнения координат, при совпадении откройте соответствующий файл с координатами, и выполняйте, а потом снова поиск…
не понятно зачем тут нужна быстрота… ну да ладно, если нужна попробуйте переместить нужные файлы с sd карты в переменные, и будет вам быстрее)))
Определитесь с требованием к точности координат. После этого выбираете формат хранения (точно не текстовый). Дальше ключевое слово для разработки алгоритма - квадродерево. Хранить сегменты реки в отдельных файлах не самая лучшая идея для быстрого поиска.
Не озвучены ограничения по памяти для алгоритма поиска (не сколько в устройстве, а сколько остается для модуля навигации).
Какие ограничения на протяженность маршрутов? Какие ограничения на размер одновременно покрываемой сетью маршрутов области? Какая локализация по широте области (далеко ли от полюса?) - необходимо ли затачиваться на всемирную работу, или это решение для рек средней полосы?
Самое первое направление оптимизации - для каждого сегмента реки в начала блока данных лежит ограничивающий четырехугольник в координатах широты-долготы. Если текущее положение внутри этого четырехугольника, то данный сегмент помечается кандидатом на точный поиск. Внутри этого сегмента в зависимости от его сложности идет разбивка на подсегменты (применяется та же методика). Дальше находится баланс между сложностью работы с вспомогательной структурой и линейным поиском.
Благодарю всех откликнувшихся! Извините за неточное формулирование задачи, писал уже с опухшей головой от 3х мерных массивов. ![]()
Попробую сформулировать задачу точнее и ответить на вопросы.
Изначально да, я думал что маршрут займет мага-гига байты и прилепил SD карту к проекту. Но когда начал “пробивать” реку, то выяснилось, что общий объем данных = 18502*4 = 7200байт, а в реальности 6Кбайт, т.к. не все файлы по 50 точек. Т.е. чисто теоретически можно попробовать запихать это во флеш ардуинки, а не на SD. Получится - отлично. Нет - придется все таки читать с карты. Но пока прошу считать что данные именно во флеше. Чтение и оптимизацию с SD пока опустим.
Да, тоже думал об этом и когда размечал маршрут, даже на карте чертил прямоугольники. Но, увы может быть ситуация, когда реальное положение этого сегмента может не попасть в прямоугольник МинШир, МинДол - МаксШир, МахДол, например на изгибе реки, когда маршрут пробит рядом с правым берегом, а кат стоит у левого. Чисто теоретически. Как тогда определять принадлежность текущего положения к этому “файлу”? Брать не сравнение координат, а расстояния до цента прямоугольника? Там формулы “дикие” с точки зрения производительности, я боюсь завязну по времени. А контроллер должен и другой работой заниматься.
Вот примерный код для определения расстояния между 2 точками: (НЕ отлаживал и НЕ проверял - пока просто скопипастил идею):
float distance(float lat1,float lon1,float lat2,float lon2) {
float p = 0.017453292519943295; // Math.PI / 180
float a = 0.5 - cos((lat2 - lat1) * p)/2 +
cos(lat1 * p) * cos(lat2 * p) *
(1 - cos((lon2 - lon1) * p))/2;
return 12742 * asin(sqrt(a)); // 2 * R; R = 6371 km
}
Почему-то криво вставилось: общий объем данных = 18 умножить 50 умножить 2 умножить 4 = 7200байт
Вам не нужно определять расстояние до точки в километрах. Для относительного сравнения расстояний считаем систему широта-долгота условно прямоугольной системой координат (поэтому я спрашивал широтность области), дальше пифагор без корня (сравниваем квадраты).
Но я рекомендую при заливке карты переводить систему координат в декартову. Т.е. работать не с широтой-долготой, а с метрами. За нулевую точку брать хотя бы центр рабочей области. Искажения из-за удаления от центра координат проекции на ваших расстояниях (тоже про это спрашивал) несущественны. Т.е. единственная тригонометрическая операция будет при приеме собственных координат и переводе их в декартовы.
Для учета погрешностей берег левый - берег правый ограничивающие прямоугольники расширяются на ширину реки. Алгоритм должен учитывать, что если нет полного попадания в область, то надо перебирать уже непопавшие в порядке убывания расстояния до границ. Но в любом случае, после перехода в декартову систему каждое сравнение - это только сложение и умножение.
И еще раз прочитайте про квадродерево. Это не то же самое, что ограничивающие прямоугольники. Это сложнее, но эффективнее.
Планировал в метрах(или в квадратах метров, чтобы корень не брать). Код функции расстояния потом исправлю, сделаю ее целочисленной.
Широтность = пока что это Москва(Рязань) - Нижний(Павлово) по Клязьме или Оке. Координаты в прямоугольнике {39.721986 - 43.062888, 54.296839 - 55.971386}. Размер прямоугольника 250х200км По реке это 400-700км.
Кажется понял. Т.е вместо хранения координат в градусах мы храним координаты в метрах от… ну, например, точки старта. Т.е. N-ная точка находится на 100500м правее и на 100300м выше. Гениально! Как я до этого не допер? Урра! Долой синусы и дробные числа!!!
Гениально-2!!! Я бы до этого точно бы не допер.
Спасибо, обязательно почитаю.
@Мишутк, спасибо Вам огроменное!!! Снимаю шляпу и выражаю благодарность! Вы реально очень помогли с реализацией проекта. Все стало просто, быстро и логично.
Итог: есть набор “файлов”(массивы) с координатами(декартовыми). Есть индексный “файл” с координатами прямоугольников(расширенный на ширину реки). Смотрим индекс - находим файл - идем по нему. Как закончился, берем следующий(или следующий(или заново отперделяемся где мы)).
Перевел, посчитал разницу в определении угла между 2 точками на удалении 1.2км: разница УголПоGPS - УголВдекартовых составил 2.5 градусов. Вот сижу и думаю, много это или мало и как это отразится на поведении ката на маршруте…
Даже не глядя скажу, у вас ошибка. Или просто в формулах математически, или потеря точности. В качестве теории - угол схождения мередиан. Это источник угловых ошибок на больших расстояниях. Грубо очень - 1 градус на 100 км при движении вдоль широты. В наших широтах ближе к 1.5-2 градусу.
В качестве базовых знаний - учебник по морской или аэронавигации. Без этой теории вы даже не сможете понять собеседника, который вам может дать советы. Ну и вопросы правильные задать.
Вообще говоря, достаточно школьного курса геометрии.
Правда, этот школьный курс нужно знать (и уметь им пользоваться), а не просто “проходить”.
А там про то, что земля круглая рассказывают? Юра на плоту до сих пор к краю земли плывёт.)
В рамках данной темы и предлагается перейти в проекцию круглой земли на плоскость. Пользуясь ограничениями на локальность (размер рабочей области). Самостоятельно из школьного курса геометрии вывести формулы перевода из географической системы счисления в гномоническую сложновато. Учебник по навигации как раз даст перевод, даст понятие об инвариантах, искажениях, погрешностях. А то поплывет вдаль по азимуту и намотается на полюс.
Отлично! Если ошибка у меня в расчетах или в моем непонимании как делать расчеты, значит это можно исправить. Попробую. Поможете?
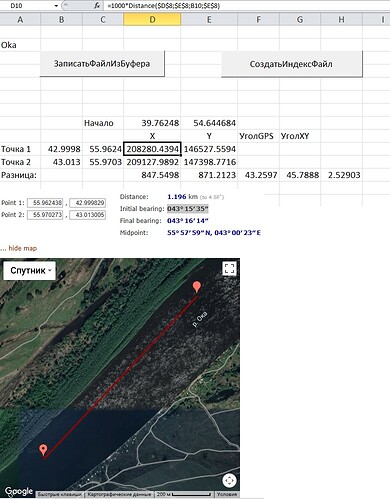
Начало 39.76248 54.644684
Точка 1 42.999829 55.962438
Точка 2 43.013005 55.970273
Начало - это точка старта, 0 в декартовой системе. Далее функцией Distance считаю расстояние по Х и по У для обоих точек. Как считаю: Для Х беру координаты начальной точки, широту начала и долготу точки. Для У беру координаты начальной точки, широту точки и долготу начала. Есть координаты ХУ двух точек. Считаю разницу d, угол = арктангенс(dY/dX) = 45.78875129
Но по онлайн калькурятору забивая туда GPS координаты получаю угол 43.25972222
Где собака порылась?
Function Distance(lon1, lat1, lon2, lat2)
P = 1.74532925199433E-02 '// Math.PI / 180
d2 = 0.5 - Cos((lat2 - lat1) * P) / 2 + Cos(lat1 * P) * Cos(lat2 * P) * (1 - Cos((lon2 - lon1) * P)) / 2
Distance = 12742 * Asin(Sqr(d2)) ’ // 2 * R; R = 6371 km //???6364.181 - на нашей широте
End Function
Function Asin(a)
Asin = Atn(a / Sqr(1 - a ^ 2))
End Function
Во первых, что и по каким формулам считает онлайн калькулятор ни я ни вы не знаете. Учитывается ли там магнитное склонение я не знаю тоже. Читайте про истиный, магнитные курсы.
Во вторых, после перевода координат в гномоническую проекцию у вас и карта (маршрут) и положение судна вообще никак с геокоординатами не связано. Вы работаете в х-у как в компьютерной игрушке на клеточках. Именно в этом суть упрощения и оптимизации. Вот зачем полезли в онлайн калькулятор? Что вам им посчитаный азимут дает, куда его в программу свою сунете?
Делайте так: начальная точка имеет декартовы координаты 0,0. Ориентация в этой точке осей по параллели и меридиану. Используете гномоническую проекцию в этой точке. Вычисляете декартову координату в гномонической проекции для второй точки. У вас все в метрах. Находите угол. На судне по компасу находите направление, корректируете на магнитное склонение и пилите по нужному азимуту на длину гипотенузы получившейся. По ходу корректируете свое отклонение от целевой точки (у вас будет угол сноса, естественно, из-за течения и ветра). Каждый прием своих координат переводите сразу в декартовы используя имеющуюся проекцию. Точку ее инициализации не меняете, по ней построена вся карта.
Для маленького судна курс (давайте так, по компасу на судне вы знаете направление оси катера) и путевой угол будут отличаться намного больше, чем вы сейчас ловите в своих “сравнениях”. Он вам будет служить всего лишь ориентиром, чтобы примерно в нужную сторону начать движение. Дальше дикая борьба с получением траектории по скачущим координатам и коррекция своего положения для удержания на оси маршрута. Вы еще не один клок волос на себе вырвете на алгоритме усреднения координат от спутника.
Есть формулы для расчета угла по координатам. Я пока до них не добрался, но видел их. Кроме того, я проверял несколько калькуляторов, они дают одинаковый результат. Вряд ли mr.John из Калифорнии будет учитывать магнитное склонение в Рязани. Но не суть. Хорошо, примем что не знаю.
Но проверит работу алгоритма мне как-то надо. Я не Бог, а всего лишь человек. И прежде чем выходить на воду пытаюсь убедиться, что моя программа работает верно. А как убедиться - ну, например, сравнить куда мы пойдем и куда рекомендуют умные дядьки.
Так я же вроде так и делаю. Ни?
Нашел угол. А верно ли я считаю - проверил. Разница 2.5 Это заставило меня задуматься…
Да, коррекция по ходу будет автоматически, т.к. 1раз в сек я получаю текущие координаты и корректирую курс. Но 2.5!? 2.5 Карл, откуда?
Сейчас убегаю, вечером проверю расхождение в угле между 0 точкой старта и самой первой точкой. Если расхождения нет - значит косяк проекции. Если есть - нужно искать откуда.
P.S. Кстати, Яндекс-карты почему-то показывают бОльшее расстояние, чем формула Хаверсина.
Такой вопрос задают преподаватели молодым морячкам или летчикам на зачете или экзамене. И ответ на него вы уже знаете где получить.