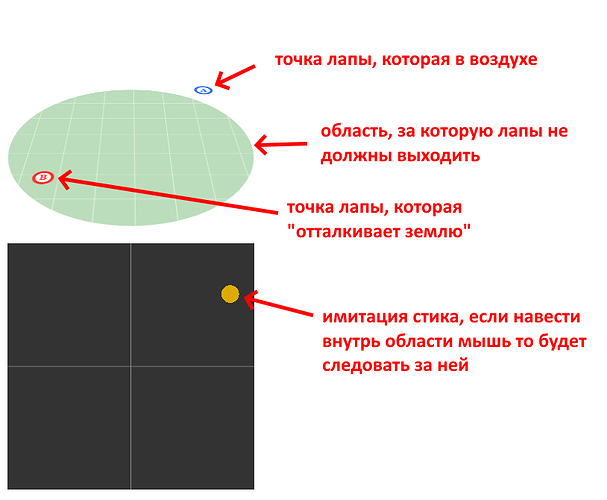
Привет! Я помню ваш вопрос. У меня как раз дошло дело до кинематики при прямолинейном движении, и чтобы не тронуться умом окончательно, прошивая раз за разом нерабочие варианты в контроллер, я накидал анимированную трехмерную html демку, в которой и обкатал алгоритм. Можете заценить. Поскольку .html тут прикладывать нельзя, могу только ее исходник привести:
<HTML>
<HEAD>
<TITLE>Bhla Bhla</TITLE>
<meta charset="utf-8">
<style>
div#circle {
position: relative;
display: block;
border-radius: 50%;
background: linear-gradient(#fff, transparent 1px), linear-gradient(90deg, #fff, #bdb 1px);
background-size: 10mm 10mm;
background-position: 0 0;
transform: perspective(140mm) rotateX(60deg) translateZ(-8mm);
transform-style: preserve-3d;
perspective-origin: center bottom;
}
div#circle>div {
position: absolute;
display: block;
width: 4mm;
height: 4mm;
font-size: 3mm;
line-height: 4mm;
font-weight: bold;
border: 1mm solid #777;
color: #777;
border-radius: 3mm;
margin: -3mm 0 0 -3mm;
text-align: center;
background: #fff;
}
div#circle>div.floating {
border-color: #37f;
color: #37F;
}
div#circle>div.landed {
border-color: #f33;
color: #f33;
}
div#circle>div#S {
border-color: #fa3;
color: #fa3;
}
div#joystick {
display: inline-block;
width: 70mm;
height: 70mm;
background: radial-gradient(circle at center, #da0 0, #da0 2.5mm, transparent 2.5mm),
repeating-linear-gradient(90deg, transparent, transparent 49.75%, #888 50%, transparent 50.25%, transparent 100%),
repeating-linear-gradient(transparent, transparent 49.75%, #888 50%, transparent 50.25%, transparent 100%), #333;
}
</style>
</HEAD>
<BODY>
<div id="circle">
<div id="A" class="landed">A</div>
<div id="B" class="landed">B</div>
</div>
<div id="joystick"></div>
<script type="text/javascript">
var right_x = 0;
var right_y = 0;
var bg_x = 0;
var bg_y = 0;
document.getElementById('joystick').onmousemove = function(e) {
var rect = e.target.getBoundingClientRect();
right_x = Math.round((e.clientX - rect.left - rect.width / 2) / rect.width * 2000);
right_y = Math.round((rect.height / 2 - e.clientY + rect.top) / rect.height * 2000);
e.target.style.background = "radial-gradient(circle at " + String(e.clientX - rect.left)+"px "+String(e.clientY - rect.top)+"px, #da0 0, #da0 2.5mm, transparent 2.5mm),"
+ "repeating-linear-gradient(90deg, transparent, transparent 49.75%, #888 50%, transparent 50.25%, transparent 100%),"
+ "repeating-linear-gradient(transparent, transparent 49.75%, #888 50%, transparent 50.25%, transparent 100%), #333";
}
document.getElementById('joystick').onmouseout = function(e) {
right_x = 0;
right_y = 0;
e.target.style.background = "radial-gradient(circle at center, #da0 0, #da0 2.5mm, transparent 2.5mm),"
+ "repeating-linear-gradient(90deg, transparent, transparent 49.75%, #888 50%, transparent 50.25%, transparent 100%),"
+ "repeating-linear-gradient(transparent, transparent 49.75%, #888 50%, transparent 50.25%, transparent 100%), #333";
}
function circle(r, dx, dy) {
var circ = document.getElementById("circle");
circ.style.height = r * 2 + "mm";
circ.style.width = r * 2 + "mm";
bg_x = (bg_x + dx) % 10;
bg_y = (bg_y + dy) % 10;
circ.style.backgroundPosition = bg_x + "mm " + bg_y + "mm";
}
function pos (el, x, y, z = 0) {
el.style.left = x + "mm";
el.style.top = y + "mm";
el.style.transform = "translateZ(" + z + "mm)";
}
function hypot (dx, dy) { return Math.hypot(dx, dy); }
function max (x, y) { return Math.max(x, y); }
function abs (x) { return Math.abs(x); }
function min (x, y) { return Math.min(x, y); }
function sqrt (x) { return Math.sqrt(x); }
// МАГИЯ ТУТ
function div (val, divider) { return divider > 0 ? val / divider : 0; }
var max_radius = 35;
var max_height = 30;
// максимальные скорость в мм/с и ускорение в мм/с², отмасштабированные до периода итераций 20мс
var maximum_velocity_value = 100 / 50; // за 1 / 50 секунды
var maximum_acceleration_value = 75 / 2500; // за 1 / 2500 секунды за секунду
// текущий вектор скорости
var current_velocity_dx = 0;
var current_velocity_dy = 0;
// координаты находящейся на поверхности конечности
var landed_limb_x = 0;
var landed_limb_y = 0;
// координаты поднятой конечности
var floating_limb_x = 0;
var floating_limb_y = 0;
// фаза
var phase = true;
function calc() {
// ПОЛУЧЕНИЕ ДАННЫХ С ДЖОЙСТИКА -1000..1000
var joystick_dx = right_x;
var joystick_dy = right_y;
var joystick_dl = hypot(joystick_dx, joystick_dy);
// получение единичного вектора желаемого направления
var setpoint_velocity_cos = div(joystick_dx, joystick_dl);
var setpoint_velocity_sin = div(joystick_dy, joystick_dl);
// получение нормализованного значения отклонения джойстика
var joystick_normalized_value = div(joystick_dl, hypot(min(abs(joystick_dx), abs(joystick_dy)), 1000));
// получение значения желаемой скорости
var setpoint_velocity_value = joystick_normalized_value * maximum_velocity_value;
// преобразование данных джойстика в вектор целевой скорости "setpoint_velocity"
var setpoint_velocity_dx = setpoint_velocity_cos * setpoint_velocity_value;
var setpoint_velocity_dy = setpoint_velocity_sin * setpoint_velocity_value;
// ВЫЧИСЛЕНИЕ ВЕКТОРА СКОРОСТИ ПРИЗЕМЛЕННОЙ КОНЕЧНОСТИ
// текущий вектор скорости "current_velocity" переходит в "setpoint_velocity" с заданным ускорением
// определение вектора из конца "current_velocity" в конец "setpoint_velocity"
var to_setpoint_dx = setpoint_velocity_dx - current_velocity_dx;
var to_setpoint_dy = setpoint_velocity_dy - current_velocity_dy;
var to_setpoint_dl = hypot(to_setpoint_dx, to_setpoint_dy);
if (to_setpoint_dl > maximum_acceleration_value) {
// если длина найденного вектора превышает значение максимального ускорения за итерацию
// вектор ускорения применяется к текущей скорости
current_velocity_dx += div(to_setpoint_dx, to_setpoint_dl) * maximum_acceleration_value;
current_velocity_dy += div(to_setpoint_dy, to_setpoint_dl) * maximum_acceleration_value;
} else {
// длина вектора меньше максимального ускорения за итерацию,
// применение вектора длиной maximum_acceleration_value вызовет перемещение дальше требуемого значения
// поэтому "current_velocity" просто приравнивается к "setpoint_velocity"
current_velocity_dx = setpoint_velocity_dx;
current_velocity_dy = setpoint_velocity_dy;
}
// ВЫЧИСЛЕНИЕ ВЕКТОРА СКОРОСТИ ПОДНЯТОЙ КОНЕЧНОСТИ
var floating_velocity_dx = 0;
var floating_velocity_dy = 0;
// текущая скорость
var current_velocity_value = hypot(current_velocity_dx, current_velocity_dy);
if (current_velocity_value != 0) {
// определение целевой позиции поднятой конечности - на краю окружности в направлении current_velocity
var floating_target_x = div(current_velocity_dx, current_velocity_value) * max_radius;
var floating_target_y = div(current_velocity_dy, current_velocity_value) * max_radius;
// текущее расстояние от центра до позиции приземленной конечности
var center_to_landed_limb_distance = hypot(landed_limb_x, landed_limb_y);
// конечность движется в направлении, обратном движению - вычисляем косинус угла между векторами landed_limb и -current_velocity
var cos = div(landed_limb_x * -current_velocity_dx + landed_limb_y * -current_velocity_dy, center_to_landed_limb_distance * current_velocity_value);
// расстояние - сторона треугольника напротив угла с найденным косинусом, к которому прилегают стороны center_to_landed_limb_distance и max_radius
var landed_to_out_distance = sqrt(center_to_landed_limb_distance * center_to_landed_limb_distance + max_radius * max_radius - 2 * cos * center_to_landed_limb_distance * max_radius);
// определение векора из текущего положения поднятой конечности в ее целевую позицию
var to_floating_target_dx = floating_target_x - floating_limb_x;
var to_floating_target_dy = floating_target_y - floating_limb_y;
var to_floating_target_dl = hypot(to_floating_target_dx, to_floating_target_dy);
// определение значения скорости поднятой конечности, необходимой чтобы успеть переместиться в целевую позицию
var floating_velocity_value = to_floating_target_dl * current_velocity_value / landed_to_out_distance;
// определение вектора скорости поднятой конечности
floating_velocity_dx = div(to_floating_target_dx, to_floating_target_dl) * floating_velocity_value;
floating_velocity_dy = div(to_floating_target_dy, to_floating_target_dl) * floating_velocity_value;
}
// СМЕНА ФАЗ ПРИ ПРИБЛИЖЕНИИ ПРИЗЕМЛЕННОЙ КОНЕЧНОСТИ К КРАЮ ОКРУЖНОСТИ
// не перешагнет ли край окружности при приращении координат на значения вектора скорости?
if (hypot(landed_limb_x - current_velocity_dx, landed_limb_y - current_velocity_dy) >= max_radius) {
// смена роли конечностей и фазы
var temp = landed_limb_x;
landed_limb_x = floating_limb_x;
floating_limb_x = temp;
temp = landed_limb_y;
landed_limb_y = floating_limb_y;
floating_limb_y = temp;
phase = !phase;
}
// ПЕРЕМЕЩЕНИЕ ПО ПОЛУЧЕННЫМ ВЕКТОРАМ СКОРОСТИ
landed_limb_x -= current_velocity_dx;
landed_limb_y -= current_velocity_dy;
floating_limb_x += floating_velocity_dx;
floating_limb_y += floating_velocity_dy;
// ВЫЧИСЛЕНИЕ ВЫСОТЫ ОТ ПОВЕРХНОСТИ ДЛЯ ПОДНЯТОЙ КОНЕЧНОСТИ
// множитель высоты поднятой конечности f(x) = 1 - (x - 1)² где x = 0..1 удаленность поднятой конечности от радиуса
var height_scale = (1 - (floating_limb_x * floating_limb_x + floating_limb_y * floating_limb_y) / (max_radius * max_radius));
// второй множитель - отношение текущей скорости к максимально возможной
height_scale *= current_velocity_value / maximum_velocity_value;
// итоговая высота
var floating_limb_height = height_scale * max_height;
// ОТОБРАЖЕНИЕ
/* актуальное значение скорости
console.log(Math.floor(Date.now() / 1000 % 100) + " velocity: " + Math.round(current_velocity_value*50*100)/100 + "mm/s");/**/
circle(max_radius, -current_velocity_dx, current_velocity_dy);
if (phase) {
pos(A, max_radius + landed_limb_x, max_radius - landed_limb_y);
pos(B, max_radius + floating_limb_x, max_radius - floating_limb_y, floating_limb_height);
A.className = "landed";
B.className = floating_limb_height > 0 ? "floating" : "landed";
} else {
pos(A, max_radius + floating_limb_x, max_radius - floating_limb_y, floating_limb_height);
pos(B, max_radius + landed_limb_x, max_radius - landed_limb_y);
A.className = floating_limb_height > 0 ? "floating" : "landed";
B.className = "landed";
}
}
var timerId = null;
timerId = setInterval(calc, 20);
</script>
</BODY>
</HTML>
скопировать в текстовик, изменить расширение на .html и запустить в браузере.
На самом деле, разумеется, точки будет не две, а шесть, и каждая в своем круге своей конечности. Но у всех четных конечностей (0, 2, 4) будет координата точки А в своем круге, а у нечетных (1, 3, 5) - координата точки В.
Почти самое главное, что кинематика здесь не просто в “попугаях” - максимальная скорость ограничена мм/с, ускорение мм/с² - все эти величины можно найти в коде. Гекса с таким управлением будет плавно разгоняться, тормозить и менять курс в любой ситуации.